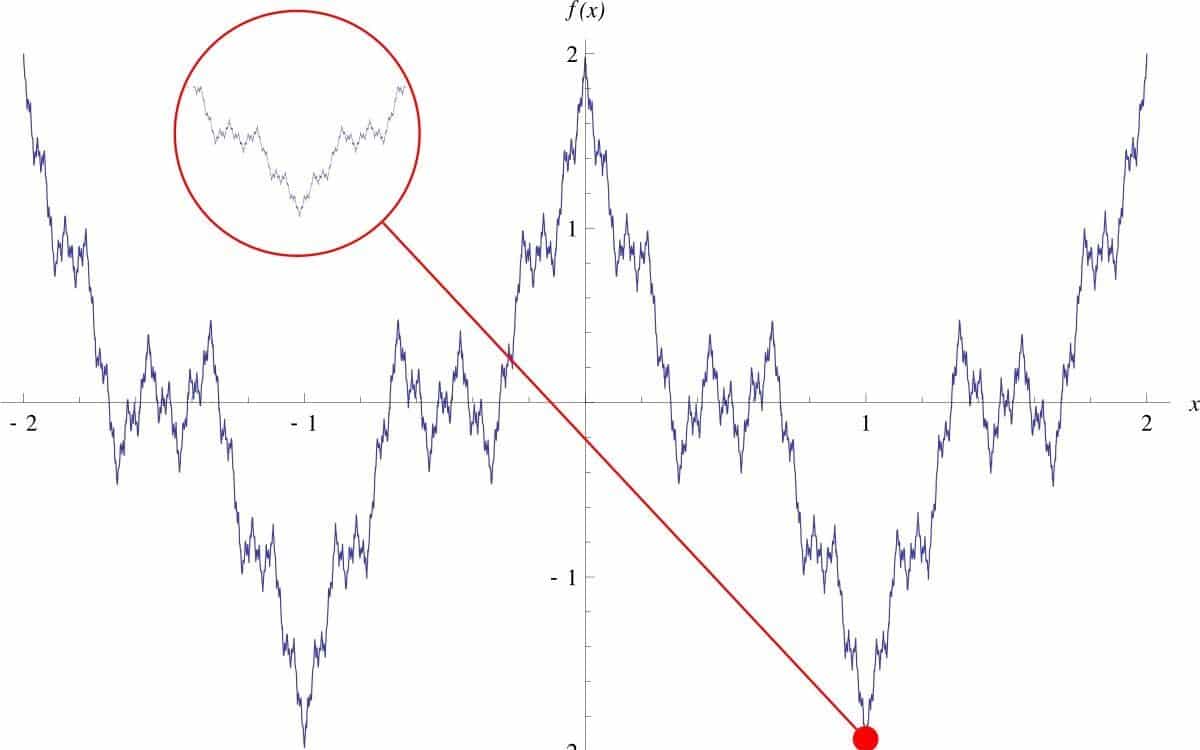
Funkcja „patologiczna” Karla Weierstrassa na zawsze przekształciła matematykę
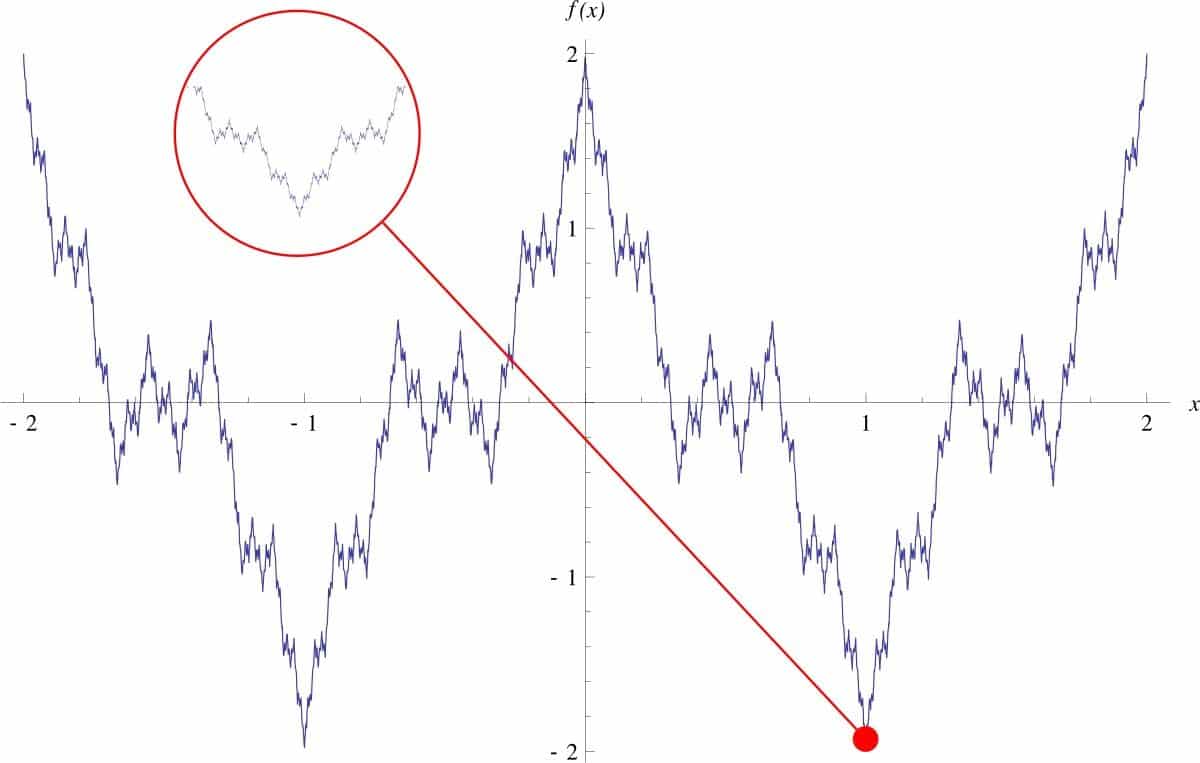
Funkcja „patologiczna” Karla Weierstrassa
Pod koniec XIX wieku Karl Weierstrass wynalazł funkcję, która została otrzymana jako „godne ubolewania zło”. Z czasem ta „potworna funkcja” ostatecznie przekształciła podstawy matematyki.
Ich podstawowe pojęcia były zakorzenione w intuicji i nieformalnych argumentach, a nie precyzyjnych definicjach formalnych. Dopóki w odpowiedzi pojawiły się dwie szkoły myślenia.
Francuscy matematycy byli bardziej zaniepokojeni zastosowaniem obliczeń do problemów fizycznych. Z drugiej strony, w dziewiętnastym wieku niemieccy matematycy zaczęli położyć wszystko poniżej. Zaczęli szukać kontraktów, które mogłyby być podobno bronić założeń i ostatecznie wykorzystać te kontreksyplos, aby umieścić obliczenia na bardziej stabilnej i trwałej bazie.
Jeden z tych matematyków był Karl Weierstrass. Po rezygnacji z studiów finansowych, Weierstrass rozpoczął karierę jako profesjonalny matematyk, gdy miał prawie 40 lat.
Jednak wystarczająco dużo czasu, aby zrewolucjonizować tę naukę, wprowadzając jedną:
„Matematyczny potwór”
W 1872 r. Weierstrass opublikował funkcję, która zagroziła wszystkim, co matematycy rozumieli o obliczeniach.
Został przyjęty z obojętnością, gniewem i strachemszczególnie przez matematycznych gigantów francuskiej szkoły myślenia.
Henri Poincaréz jednej strony, nazwał nowe odkrycie Weierstrass „Oburzenie zdrowego rozsądku”.
Charles HermiteZ drugiej strony nazwał go „MAL GOLOBOLODE”.
Aby zdać sobie sprawę, dlaczego wynik Weierstrass został tak źle przyjęty, sugeruje, że zaczynamy od zrozumienia dwóch najbardziej fundamentalnych koncepcji obliczeń:
Ciągłość
Funkcja ciągła jest dokładnie tym, co się wydaje – funkcja, która nie ma odstępów ani obcasów. Możliwe jest narysowanie ścieżki dowolnego punktu tej funkcji do dowolnej innej bez podnoszenia ołówka.
Obliczenia ma głównie określanie, w jaki sposób zmieniają się funkcje ciągłe. Działa ogólnie, zbliżając się do danej funkcji z Linie proste i nieformalne.
Różnica
W dowolnym momencie tej krzywej można narysować linię „styczną” – linię, która najlepiej przychodzi do krzywej w pobliżu tego punktu. Nachylenie lub nachylenie linii stycznej mierzy, jak szybko zmienia się funkcja w tym momencie. Może zdefiniować inną funkcję, zwaną pochodną, która zapewnia nachylenie linii stycznej w każdym punkcie jej pierwotnej funkcji. Jeśli pochodna istnieje we wszystkich punktach, mówi się, że pierwotna funkcja jest zróżnicowana.
Funkcje zawierające nieciągłości nigdy nie są zróżnicowane.
Oznacza to, że nie będzie możliwe narysowanie linii stycznej, która zbliża się do nieciągłości, co oznacza, że twoja pochodna nie będzie tam istniała. Ale nawet funkcje ciągłe nie zawsze są zróżnicowane we wszystkich punktach.
Nie zakłóciło to większości dziewiętnastego matematyków. Widzieli go jako izolowane zjawisko. Powiedzieli, że funkcja jest ciągła, może istnieć tylko skończona liczba punktów, w których pochodna nie jest zdefiniowana. We wszystkich innych punktach funkcja musi pozostać przyjemna i gładka. Innymi słowy, funkcja może dokonać zygzaków i zagues tylko do pewnego punktu.
A może nie …
W rzeczywistości w 1806 r. Wybitny francuski matematyk, André-Marie AmpèrePowiedział, że udowodnił ten fakt.
Przez dziesięciolecia jego rozumowanie nie dotyczyło… aż do „Monrist the Weirstone”.
Weierstrass odkrył funkcję, która zgodnie z testem Ampère powinien być niemożliwa: Ciągłe wszędzie i nigdzie się nie różnicowane. Zbudował go nieskończenie dodając wiele fali „cosinus”.
„Funkcja patologiczna”? Koszt jest wierzyć
Wielu matematyków odrzuciło tę funkcję. „To była anomalia” – powiedzieli. Ponadto, Nie mogłem nawet tego wizualizować. W rzeczywistości na pierwszy rzut oka, próbując narysować wykres funkcji Weierstrass, wydaje się ono ciągłe w niektórych regionach.
Tylko z Zoomem widzisz, że te regiony są również „serwowane” i że będą nadal być jeszcze bardziej serwisowe i źle się zachowują – jak nazywają matematycy „patologiczny” – Z każdym dodatkowym rozszerzeniem.
Ale Weierstrass udowodnił bez marginesu za wątpliwości To, chociaż jego funkcja nie miała nieciągłości, nigdy nie była zróżnicowana.
Aby to zademonstrować, zaczęło się od przeglądu definicji „ciągłości” i „różnicowości”, które zostały sformułowane dziesięciolecia wcześniej przez matematyków Augustine-Louis Cauchy i Bernard Bolzano.
Jak pisze magazyn Quanta, definicje te były oparte na niejasnych opisach, w prostym języku i niespójnym zapisie, co ułatwiło ich nieprawidłowe interpretację. Dlatego Weierstrass przepisał je, używając precyzyjnych języków i konkretnych formuł matematycznych.
Dzięki temu było w stanie udowodnić, że w każdym momencie jego nowa formalna definicja pochodnej funkcji nigdy nie miała wartości skończonej; „Rozbił się” zawsze w nieskończoność.
Właściwymi słowami: Ciągłość nie oznaczała zróżnicowania.
A jego funkcja była naprawdę potworna, ponieważ matematycy mieli „strach”. Jako „kara” byli zmuszony do podążania śladami Weierstrass.
Weierstrass to ujawnił Matematyka jest pełna potworów: Funkcje, które wydają się niemożliwe, obce obiekty, dzikie zachowania itp.; A jego funkcja miała ostatecznie wiele praktycznych zastosowań.
Na początku XX wieku fizycy chcieli Przestudiuj ruch Brownalosowy ruch cząstek w cieczy lub gazu. Ponieważ ruch ten jest ciągły, ale nie gładki – charakteryzujący się szybkimi i nieskończenie małymi fluktuacjami – funkcje takie jak Weierstrass były idealne do modelowania.
Podobnie funkcje te zostały wykorzystane do modelowania niepewności w sposobie podejmowania decyzji i podejmowania ryzyka, a także Zachowanie rynków finansowych.